Unlocking more efficient design with Secondmind open source tools 

In this technical blog post, we examine a recent project where Secondmind worked with sustainable technologies company Reaction Engines to optimize the design and development process of heat exchangers used in its hypersonic Synergetic Air-Breathing Rocket Engine (SABRE) programme.

The collaboration aimed to significantly reduce the computation time associated with large numbers of optimization iterations with highly complex models, and help unlock better, more accurate designs.

It’s a real-world case study for our open source (OS) tools, demonstrating how we can help engineers manage the trade-offs they face during the design and development stage of engine parts, while reducing the number of design iterations required.

The heat exchangers

SABRE is a hypersonic precooled hybrid air-breathing rocket engine. The engine relies on a heat exchanger capable of cooling incoming air to -150 degrees Celsius to provide oxygen for mixing with hydrogen. This mixture then provides the jet thrust during atmospheric flight before switching to tanked liquid oxygen when in space.

During the design of this heat exchanger, Reaction Engines used aerothermal modelling and the company asked for Secondmind’s support with what was, essentially, a multi-objective optimization problem.

The SABRE heat exchangers are a lightweight, compact and highly thermally efficient technology capable of operating in the most extreme of environments. SABRE’s precooler is verified at Mach 5 supersonic flight conditions.

Side-on view of the heat exchanger

For this problem, the geometry of the heat exchanger in question comprised of nine parameters:

1. Transverse micro-tube spacing
2. Longitudinal micro-tube spacing
3. Micro-tube diameter
4. Number of tube rows in a module
5. Number of tube-side passes
6. Number of modules
7. Heat exchanger axial length
8. Heat exchanger radius
9. Heat exchanger duct radius

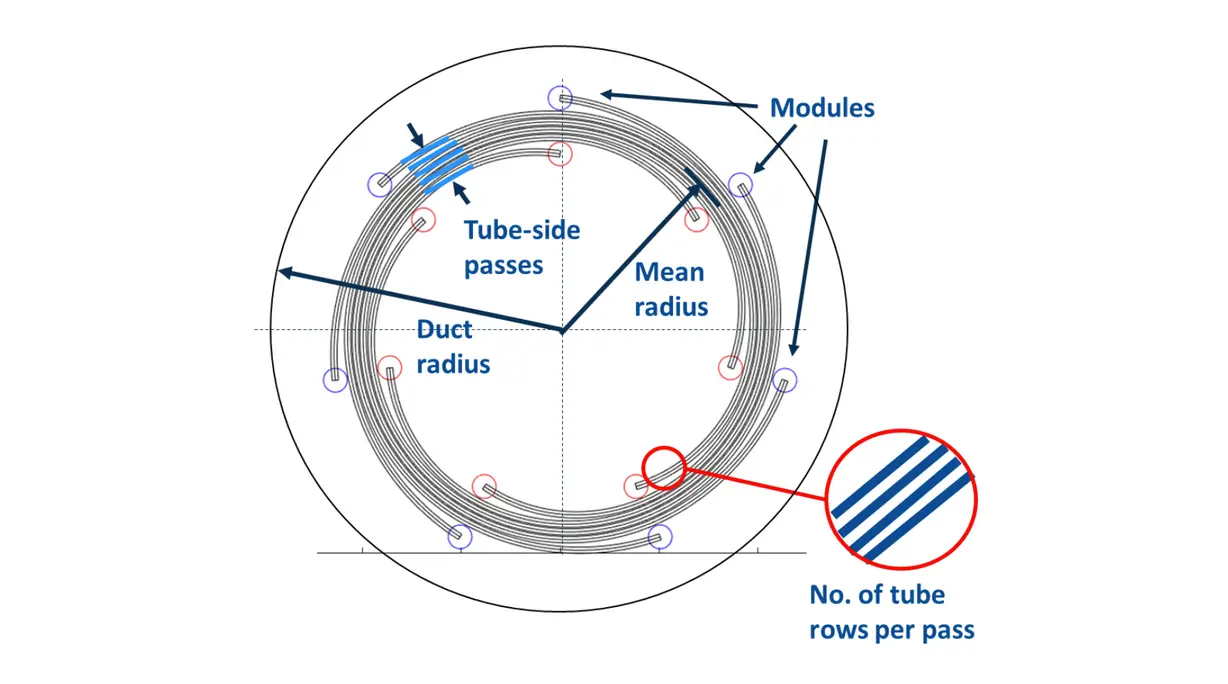
Schematic top view (along the axis) of the heat exchanger

The heat exchangers are also highly scalable by design where both the overall dimensions and the internal geometry of the exchangers can be changed.

This provides a highly adaptable design and during the design process there are many complex trade-offs to be taken into account. For example, the geometrical parameters and the fluid stream boundary conditions could be mapped onto a particular set of performance characteristics using aerothermal analysis. However, because this includes coupling the heat transfer and fluid dynamics, the resulting mappings are highly non-linear and, often, counter intuitive.

Exchange rates are another key parameter, where the amount of expendable mass to save one Pascal of pressure loss must be decided upon. But the exchange rates between performance metrics are often unknown and, as such, generate trade offs between multiple performance metrics (such as mass, pressure drop and heat load).

During our collaboration with Reaction Engines, this challenge was addressed as a multi-objective optimization problem using a mixture of discrete and continuous parameters. Boundary conditions, performance requirements and a set of constraints were supplied and the Pareto front set of solutions were the desired output for the heat exchanger designs.

Introducing ATOM

ATOM, which stands for Aero Thermaloptimization Model, is Reaction Engines’ stochastic optimization software, which relies on a number of experimentally derived heuristics. While not guaranteed to yield truly optimal results, historically, it has produced more than satisfactory results and far exceeds manual analytic approaches to design optimization, even if the number of iterations required for convergence is large.

This approach is viable for fast, 1-D performance models, where tens or hundreds of thousands of evaluations can be performed each day. However, for more expensive evaluation functions such as 2-D and 3-D computational fluid dynamics (CFD) models, this approach is not feasible due to the excessive computation time associated with the large number of iterations required for convergence.

It was therefore desirable to improve the optimization process to minimize the number of required iterations.

Introducing Bayesian optimization

Bayesian optimization (BO) sits at the heart of Secondmind’s Active Learning technology. BO is an increasingly popular method for the optimization of systems plagued by expensive and noisy evaluations because it can find solutions within heavily restricted evaluation budgets. This makes BO a very natural tool to tackle the heat exchanger design problem.

In a nutshell, BO uses fast-to-evaluate probabilistic surrogate models to predict the values of each of our multiple objectives at previously unobserved configurations.

Heuristic search strategies (known as acquisition functions) then use these predictions to guide the optimization, typically focusing resources into evaluating configurations where there is either high uncertainty or where we have particularly promising predictions — a balancing act known as the exploration-exploitation tradeoff.

BO is a very popular topic in machine learning research, and a very large number of algorithms are now available to tackle an equally large number of situations. However, the main difference between academic problems and real-world ones, is that in the former a single challenge is tackled at a time and solved in isolation. In the latter, many practical challenges arise and need to be solved all at once.

The heat exchanger design problem was no exception – and it was a great way to test and improve the flexibility and modularity of Secondmind’s OS tools. Here are the steps we took.

Step one: Dealing with multiple objectives

We have multiple competing objectives and so we do not wish our optimization to provide a single solution, rather the Pareto set of solutions summarising the potential tradeoffs between the different objectives. The Pareto set can be easily extracted from the surrogate models of each objective maintained by BO.

To apply BO to the heat exchanger design, we followed recommendations in the literature and used Gaussian processes as our surrogate models and the Expected Hyper-Volume Improvement (EHVI) acquisition function. EHVI guides the optimization to evaluate the points that we think will yield the largest improvement in our Pareto front. It was also shown great empirical success across a range of domains and problem types.

Step two: Satisfying multiple constraints

Valid heat exchangers must satisfy certain physical constraints. However, evaluating the validity of a particular configuration is expensive and not known a-priori. By building additional surrogate models that can predict if the constraints are going to be satisfied for any candidate configuration, BO can direct the search to avoid infeasible configurations.

To accommodate for constraints, we employed the classical approach consisting of fitting a GP regression model to each of the outputs defining a constraint, then using those models to predict the probability that each output would be below the required threshold, and finally multiplying EHVI by the probability that all the constraints are satisfied.

Step three: Handling simulation crashes

Occasionally, ATOM fails to return an answer, either because the configuration we query is geometrically impossible, or because it leads to numerical instabilities. So, we treated this as a “hidden” binary constraint.

We used a Gaussian process classifier (GPC) to learn which regions were leading to crashes and inform our BO algorithm where not to go. Since a GPC returns a probability, it fits naturally in our framework.

Step four: Incorporating preferences

Reaction Engines do not need to find the entire Pareto front of the problem, as extreme trade-off solutions (where the design is entirely in favour of one objective above the other), although optimal from a strict mathematical point of view, never constitute an acceptable final design choice. We incorporated this preference by setting the reference point for the EHVI criterion such that our BO algorithm would simply ignore the edges of the Pareto front and concentrate its learning on the central part.

Step five: Accommodating mixed input space

While most BO problems in the literature deal with continuous input variables, ATOM has a variety of both discrete and continuous ones. Thankfully, our OS tools allow us to deal with such situations, with a particular construct of input (search) spaces, and a bespoke acquisition function optimiser well suited for mixed input spaces.

The result

The data caption

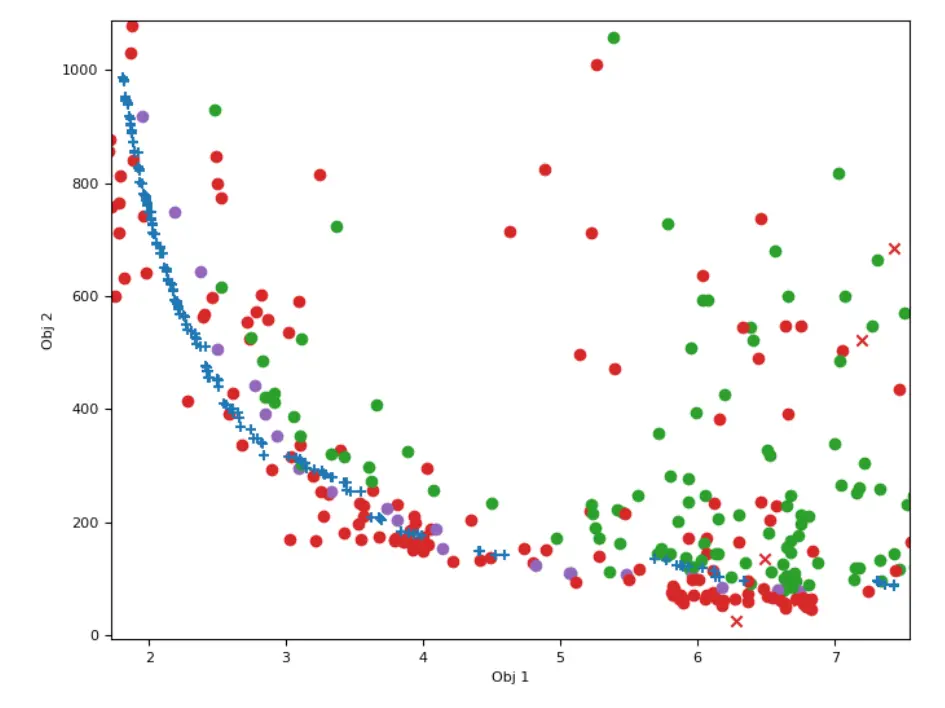
Here we present the the Pareto front obtained after running BO for 300 evaluations on Reaction Engines’ 1D heat exchanger problem. We plot the performance of each tested configuration for each of the two objectives of interest. The x axis (Obj 1) corresponds to the mass. The y axis (Obj 2) to the pressure on the side of the heat exchanger’s outer shell.

Valid points are in green and invalid ones that violate a constraint are in red. We started the algorithm with 100 randomly designed configurations (x crosses) and allowed the BO to choose 300 further points (dots).

The final Pareto front found using BO is highlighted in purple. The blue (+) crosses correspond to the Pareto front found with ATOM. Both fronts are roughly comparable, ATOM being slightly better for small mass solutions while BO finding slightly better solutions for low pressure. However, to achieve this BO required multiple orders of magnitude fewer observations! While ATOM’s optimisers are well-suited for simple models, this study has demonstrated that BO may be a key to tackle much more expensive problems.

All of the experiments made as part of this study were completed leveraging Secondmind’s open-source tools: GPflow for Gaussian process modelling, and Trieste for Bayesian optimization. But tackling the heat exchanger problem required updating and improving those tools, in particular to offer the appropriate interoperability between the different scenarios, including multiple objectives, constraints, hidden constraints, and mixed input spaces, to name a few.

This work is, therefore, a key demonstration of how machine learning experts can use these toolboxes essentially as building blocks to generate solutions to today’s pressing engineering problems.

In conclusion

In this blog post, we have highlighted how Secondmind and Reaction Engines worked together to optimize a complex design process where multiple trade offs are managed with minimal iterations.

This is an example of how engineers can benefit from the latest machine learning technologies to significantly speed up the design and development process of complex engine parts.

These open source tools are just some of the building blocks used in Secondmind Active Learning, which has been built from the ground up to solve highly complex, multi-dimensional design and development problems. And thanks to this work, our OS tools have progressed to help us work with more partners and their engineering design and development problems. The approach taken, presented in this post, can also be applied to other engine designs both in the aerospace and automotive sectors.

If you’re looking for a partner that understands how the latest, state-of-the-art machine learning can be applied to help you meet the design challenges of today and tomorrow, please get in touch.