Fergus Simpson
3 May 2023
The worlds of artificial intelligence and art are colliding. You might not expect it, but this has had an impact on our work at Secondmind and has the potential to support our mission to help automotive engineers design tomorrow’s vehicles more efficiently.
One of the great things about working in the field of machine learning is the research community that you become a part of. Everyone is working together to improve the many different technologies that sit under the hood of our machine learning tools. And with that, there is often a crossover between applications, industries and machine learning processes.
A paper authored by a team of Secondmind Labs researchers, led by Vincent Dutordoir, and in collaboration with Zoubin Ghahramani of Google, has been accepted for ICML 2023. It explains how generative AI techniques used to synthesise remarkably high-quality images (DALLE-2 and Stable Diffusion) can also be exploited to revolutionize various aspects of data science, such as the way engineers use machine learning to design and develop new cars.
DALL-E for data
There are many online art tools available, which use machine learning in some form or another. One example is DALL-E 2, where you type a descriptive line of text into the online program to create a realistic image. It’s a fun tool, but there are serious implications for the wider field of machine learning.
Image generation models such as DALL-E 2 and Stable Diffusion, show the remarkable potential that diffusion models have for retaining complex, rich probability distributions. There are likely many other applications where diffusion models can offer powerful results. In our recent paper with researchers from the University of Cambridge, we have demonstrated that Bayesian inference is one area where diffusion models can excel. We like to call this approach “DALL-E for data”.
Using underlying technology similar to DALL-E 2, which generates images based upon some input text, we demonstrate how to generate numerical predictions based upon input data points. In other words, where DALL-E 2 inputs words and outputs images inspired by those words, we are inputting numbers and outputting functions that are consistent with those numbers.
This helps overcome a key challenge when analyzing data, especially data in higher dimensions, which can be time-consuming and require a great deal of effort to be invested when modelling.
Instead, this process creates realizations of functions that could fit the data, based upon what it has learned in the past. This can be trained to replicate the behaviour of Gaussian processes but, unlike Gaussian processes, our process does not need to be trained to match each dataset, representing significant savings in terms of both time and computational resources.
So, when some data is received, the model does not have to spend a significant amount of time training to learn from that data. Instead, using our new process, the model has already been trained in the past and does not need to spend time relearning anything.
Introducing our Neural Diffusion Process
Gaussian processes (GPs) are a powerful framework to define distributions over functions, providing consistent predictions even with sparse data.
Neural network (NN) based generative models can also learn a distribution over functions, effectively mimicking GPs and reducing the computational resources required during the training process.
Many such models already exist, including Neural Processes (NPs) and Gaussian NPs. The aim of this work was to improve these methods by extending an existing state-of-the-art NN-based generative model.
Our novel model is called the Neural Diffusion Process (NDP) and it extends the use case of diffusion models to stochastic processes, allowing it to describe a rich distribution over functions.
In effect, our NDP mimics Gaussian processes, executing the mathematics behind GPs in a more efficient way. It combines the power of neural networks and Gaussian processes.
We ran several experiments to test our NDP, all of which are available in the paper. However, one result worth highlighting is that NDPs can be used in high-dimensional problems.
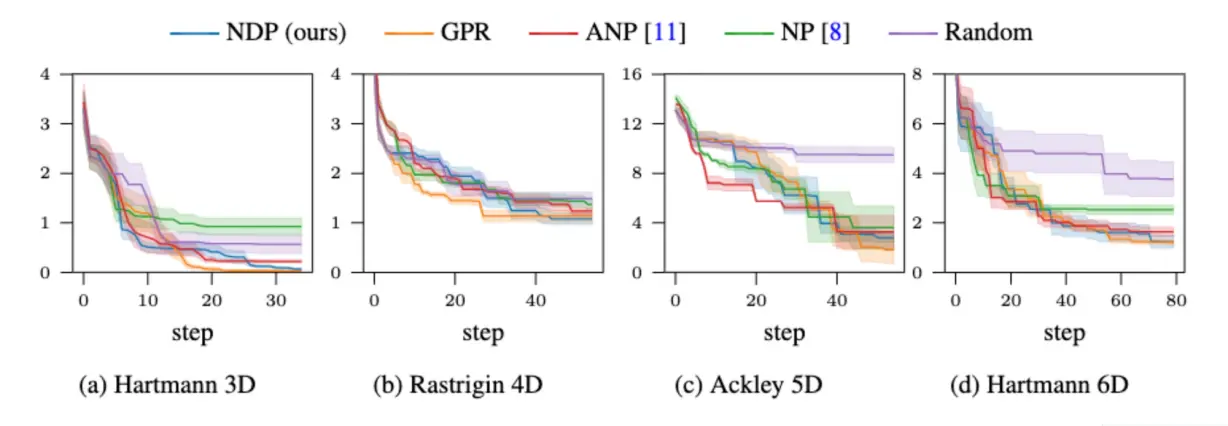
When evaluating 3D and 6D minimization problems, we discovered that NDP almost matches the performance of GPR, which is the gold standard model on this type of task. The important difference between GPR and the NDP is that the NDP requires no training during the Bayesian optimization loop, whereas the GPR needs to be retrained at every step.
The results are shown in the figures below: the regret of different probabilistic models used in Thompson sampling based Bayesian Optimization on a Hartmann 3D, Rastrigin 4D, Ackley 5D and Hartmann 6D problem. The uncertainty estimates are based on repeating the experiment five times with different random seeds.
Our NDP is an exciting addition to our toolkit at Secondmind, helping us to further optimize our machine learning tools and provide engineers with faster and more accurate predictions. If you’d like to find out more about our work and how we’re helping machine learning researchers and automotive engineers find the right solutions, click here.